|
Home Page
Six Transistor Cache
Investors
Launch Date
Contacts
Terms and Conditions
_________________________
|
Digital Quantum Computer TM
A Digital Quantum Computer With Easy To Learn 3 Command Programming Language

- A Digital Quantum Computer imports a number of features found in the quantum computing world, and implements it digitally.
- The rational for Digital Quantum Computer is based on very precise physics. We know atom based quantum computers can be made but adding each qbit demands greater precision which is implemented through averaging and noise reduction by cooling the atomic systems. This is similar to construction constraints of analogue computers where pursuing ever greater accuracy requires higher precision components until we are forced to give up.
- We moved on from analogue computer by choosing digital computers. Digital computers can be made arbitrarily precise in exchange for slower processing. The more precision, the slower the digital computers become. But there usually comes a point where a given resolution is good enough approximation to a desired answer that we can use it without needing to go to higher accuracy.
- Digital Quantum Computer follows the same rational but increasing the number of qbits under for speed and resolution has a cost. Hardware doubles in size for every qbit added. So there is technically no hope for a Digital Quantum Computer to win against an analogue Quantum Computer, but based on physics of real matter, an analogue quantum computer made with atoms cannot win the race for more precision either to deliver say a 500 qbit resolution quantum computer.
- To add to our woes, going digital with a quantum computer is at first a step backward in terms of just about everything that can be said about computing, speed, cost, development overheads. But as soon as the first few hurdles are overcome, the results are absolutely fantastic and will beat any Von-Neumann CPU architecture and any atom based quantum computer by a proverbial mile. On the bright side, these hurdles are not technical hurdles - they are infrastructure hurdles.
- That is why a Digital Quantum Computer is worth pursuing.
- To understand a Digital Quantum Computer, first we have to first methodically define what we are importing from the world of atom based quantum computing, and more importantly how we interpret those phenomena.
Entanglement Import
- To build the world's first Digital Quantum Computer, we are going to import Entanglement.
- Entanglement at the atomic level means if you create an object such as an electron with a positive spin, you automatically create and electron of the opposite spin. Regardless of distance, when you determine the direction of the spin in one electron the other electron is instantly pushed into the opposite state. It is said spin cannot be determined on its own because it is said to be in both states at the same time, and entangled which means when it is determined, the opposite state is forced on the other electron.
- Unfortunately, we cannot use this interpretation to make any useful devices. For starters we cannot force one state to be of a particular spin direction to force the other electron to take on the opposite value and thus build a machine that communicates faster than light.
- The fact that we cannot communicate faster than light to modulate an entangled pair suggests something is wrong with the interpretation.
- To get around the limitations of current interpretation, lets do a thought experiment to see if there are alternative versions of interpreting entanglement that is more practical.
- Supposing we separate a pair of gloves using a robot in a darkened room and and then mail one half to a physicist and keep one for ourselves in a box.
- Wait a few days for the mail to arrive and then physicist opens the package. If he got the left glove, then we MUST be left with the right half. And vice versa. There is no faster than light speed communication involved when arriving at the conclusion. There is also no way to force your half to be in one state or the other and thus force the physicist to receive the opposite copy. So you cannot modulate this entangled parcels even though it has spread itself across time and space and the entanglement lasts for many days. More importantly, we need to ask WHEN did the entanglement take place? The entanglement happened at the instant when the robot separated the gloves.
- At this point, it is possible to turn to the 'Copenhagen interpretation' AND 'Bell's theorem' to explain entanglement is not as described above. But look carefully, there are two conditions at work. The concept that connects or does not connect between them is WHEN and WHERE did entanglement take place? That specific issue of time and place is overlooked because the subject is complicated already, but it unravels everything. The issue of WHEN and WHERE entanglement took place is important. Either entanglement took place at a time before the wave function collapsed, or entanglement happened at the same time the wave function collapsed. If entanglement occurred before the collapse of the wave function, then Bell's theorem result is correct but without needing magical communications schemes. If entanglement occurred at the same time the wave function collapsed, then Copenhagen interpretation combined with Bell's theorem is correct. We know for sure entanglement occurred before the collapse of wave function took place. Otherwise the apparatus for creating entanglement did not work.
- Looking at the glove problem, we need to rethink what is happening and then assume that physical observation of entanglement is different to what we originally thought it was.
- Firstly, the two gloves are not in a supposition of states. Their state was remembered at the time the gloves were separated. It doesn't matter thereafter whether we can read the state or not, what is remembered cannot be changed. When we check one of the gloves, the other will be exactly the opposite of what we have in our hand. This is true only in terms of physical experience because we are embedded in the physical universe which does not produce a different result at any time, despite underlying physics that could be completely different, and therefore, at present any alternative explanations are of no interest to Digital Quantum Computer design.
- With this real world interpretation of entanglement (despite Bell's maths supported by physics), we can magically leap forward to get a Digital Quantum Computer built. In a digital context entanglement means noting something down to remember it for later use even if time and distances separate those events. For a Digital Quantum Computer, that simple statement means a lot and fundamentally alters the architecture of a computer. We don't need Von-Neumann, Turing Machine or Boolean logic to make sense of computation. Every last thing that is a computational function can be distributed and entangled and still work 100% so long as the computation functions we use are entangled.
- It will take a while for that to sink in under lots of examples, but essentially it frees us from having to think about computing as something that is inside a Von-Neumann machine, or is following Turin Machine or is reliant on Boolean logic to function.
- This is an extremely important observation because in a quantum computer, there are no Von-Neumann machines, there is nothing in a sense that follows a Turin-Machine and there is no Boolean logic to fall back on and yet quantum computers can compute.
- [ A Digital Quantum Computer ultimately reduces to a state machine running in Branchial Space and obeys all its maths. Entanglement is required for causal invariance. Despite entanglement and causal invariance, a Digital Quantum Computer can produce information black holes as machines becomes larger. One method of forming information black holes in large computational systems is the implementation of communication timeout features. Avoid as best as possible. Another possibility is race conditions which are not entangled. Most local variable data cannot be entangled because of the high cost of entanglement hardware that reduces overall data processing per chip unit area. It is a balancing act. As much as possible, a Digital Quantum Computer should entangle shared (non-local) data so as not to behave differently over time and break causal invariance, at the same time forgo entanglement for local variables and local digital communications to increase computational power per unit area.]
- [ Smallest fundamental computational objects in Branchial Space are estimated to be 10-199 in size. At these sizes computational irreducibility sets in. We being much larger live in computational reducible pockets where all individual atoms and sub atomic particles play out their behavior, and their behavior can be worked out. This behavior is thought to be reproducible by the state changes in machines 10-199 in size. This model still imparts a human centric view of size and proportionality. Branchial Space offers a way out by allowing the objects of size 10-199 being themselves made of computational units 10-199 smaller and engaged in much faster state changes. Likewise objects at our scale may be slow running computational units in a bigger space 10199 in size. And those objects may yet be part of machines that 10199 bigger. The idea is there is no special relative size where humans and our universe exist. We could easily be just one layer of many layers of 10199 scales above and below our current level. The only thing that needs to be real are the state changes in cellular automata that happens at higher and higher frequencies to render the universe. There could be billions upon billions of devices that change state, but one single CPU can go around changing state taking eons to do so for each complete state change for the entire system. We being stuck in the fabric of the state machines in Branchial Space would not become wise to any of that. ]
Supposition of States Import
- Recapping the previous import, we had to be careful about what we import from the quantum world into the Digital Quantum Computer, and it is important be very precise of the interpretation of quantum phenomena.
- The next item we import is the idea of supposition of states. In a real quantum computer supposition of states and collapse of the wave function to a specific answer contains some harsh realities. A single quantum bit potentially stores an infinite amount of information because it contains all known states. This is not practical in a digital interpretation. Instead what we do is count the number of distinct states that we want to use. In a real quantum computer the same limitations apply because we need to cool the atom that stores the information to ever smaller temperatures and/or average readings over a longer time period to be able to pick out distinct states. Potentially an infinite amount of cooling hardware and/or and infinite amount of time is needed before we can get to extreme precision. Digital implementation of quantum bit has similar problems. To double the resolution, we need to add one more bit, and that instantly doubles the hardware. So to be practical we have to restrict ourselves to small numbers such as 8 bits which codes for 256 different states, or 16 bits that codes for 65536 distinct states.
- We need to understand how bit sizes matter with a practical problem. Suppose we want to sort n numbers where the range of the number is between 0 and 255. This range is comfortably coded by 8 bit accuracy digital quantum bit. An 8 bit accuracy digital quantum bit based Quantum Sorting Machine will take n sort operations to sort n numbers providing each number can be coded by an 8 bit accurate digital quantum bit. This is a remarkable result since sorting time is linear in n and is unaffected by how big the collection of numbers are. Best and worst case performance is n. Compare that to all the algorithms detailed in https://en.wikipedia.org/wiki/Sorting_algorithm. There isn't algorithm where best and worst case is n. The caveat we forgetting is that this is an integer machine. And/or that the number is range limited. To include bigger numbers, say numbers from 0 to 65535, then we need to add 8 more bits, or total of 256 times as much hardware to implement the algorithms. This is a huge limitation. If we scale up to 32 digital quantum bits, the hardware requirements is multiplied by 2^32 or around 4 billion times.
- Thus in order to make a practical Digital Quantum Computer, we need to restrict our state sizes to something convenient such as 4 bits, 8 bits, 10 bits, 12 bits, 14 bits, 16 bits accuracy per quantum bit. All the other sizes possible, but we don't want to spread ourselves too thin by catering to every bit size. We look at each problem and decide what is the lowest accuracy we need to solve a problem. If there are systems where the number of objects is very large - example a database with 100 million distinct names, the digital quantum accuracy bits have to be increased and the hardware multiplied upwards to be able to handle the data. For a lot of practical systems, there should be no difficulties if we can reduce the number of distinct items that need to be processed. For Big Data, the current off the shelf components such as gigabit DRAM and FPGA are good enough to handle up to 32 bit accurate quantum bit. With the best off the shelf components we should be able to build a Digital Quantum Computer to do a database query of 1 billion rows in about 1 second. Practical limitations of DRAM will lengthen the delay to 50 seconds. But then again it is a Digital Quantum Computer and simply splitting the problem down and adding 50 more Digital Quantum Computers would bring that result back down to 1 second. An equivalent result implemented with PCs would require thousands of PCs and a data center. There is added doubt whether all the inter CPU communications and network traffic would help or hinder.
State Transitions Import
- Once again from previous two imports we need to be just as careful of the next import. It gets harder to sift out what it is we must import and what we should discard.
- State to state transitions come about because quantum systems like atoms have many quantum states, and there are rules about how an atom may transfer from one state to another state. Unfortunately, the state to state transitions in real quantum systems are fixed in stone. It is simply not possible to transition a quantum system from one desired state to the next of our own choosing. So at the moment we do the next best thing which is to note down which states a new state transition can take place and force it into that state based on a conditional test. When we read back a state, we will then know the quantum computer has made a decision according to the programming. It also unfortunate that this practice is subject to error, noise and high cost. We can also bend the problem space to suit the solution space. But that requires teams of mathematicians to implement the programming which is not scalable.
- The practical realities of not being scalable hits home when we try to implement quantum annealing machines. Each type of annealing is different. But if the problem cannot be reformulated in terms of state to state transitions of atomic systems, then there is nothing to anneal. Claiming it can be done with teams of academics is not an answer either. The problem needs simple practical programmers and tools similar to how a graduate uses Python to solve every day coding problems.
- In a Digital Quantum Computer, we can facilitate an infinite number of arbitrary state to state transitions. Also we can precisely control each state to state transition without noise. Precision controlled state to state transitions in a Digital Quantum Computer versus inflexible state to state transitions in a real quantum computer. We are being spoiled here for choice. We think we go with precision controlled state to state transitions in a Digital Quantum Computer as mechanically rigid inflexible state to state transitions is just too restraining for general purpose computing. Digital Quantum Computers come with a simple 3 command (rest being flat functions) language to program. This is a practical solution being developed now.
Results
- We calculate it is possible to build a Digital Quantum Computer using simple micro-controllers with a lot of IO pins. The large number of IO pins allow for interconnect. The firmware allows for simple logic gate simulations to be done in software. We are going to use a 144 pin CPU Hypercube board to implement the firmware and the interconnections like this board under development - https://hellosemi.com/hypercube/pmwiki.php?n=Main.144pinarmcpu
- The chips are under powered, and run dog slow due to firmware instead of ASIC, but they can be paralleled :)
- We just need to parallel a dozen or two and a couple of revisions of PCB with better chips before we are beating an Intel 5GHz PC processing big data :)
- For Big Data, digital entanglement creates 100% transactional integrity when applied correctly.
- A Digital Quantum Computer supports supposition of all states which means it tries to do everything at the same time. Computing in an orderly way is implemented by adding delays and entanglement.
- A Digital Quantum Computer is 100% real-time and clockless with correct use of entanglement. This idea easy enough to understand as a Digital Quantum Computer will attempt to run all functions at the same to realize the full potential of computing by supposition of all states. It does not need clocks to do this. This idea of clockless operation extends all the way into implementation logic. The new methods are a total devastation to anyone who ever architectured a chip using clocks and much quicker to turn into working silicon. It doesn't matter if sections of the system is running at terahertz speeds and other sections thousands of time slower. Entanglement ensures state transitions do not trip over each other. This is actually a fantastic result. We have a new way to design chips that from the beginning ignores the idea that complex digital systems such as microprocessors have to be built with clocks.
- (Analysis of the details of implementation of above statements also leads us to a richer understanding of our universe. It may explain why our universe has entanglement and time - otherwise the universe can be born as a supposition of all states and everything that is, was or will be happens at the same time and there would be nothing around to 'admire' it. May be such universes are born and perish all the time in a multi-verse. It is a completely different type of multi-verse brew pot where universes can be born without machinery for implementing time or entanglement. Only universes born with machinery to implement both time and entanglement stick around long enough to be 'admired'.)
- Digital Quantum Computers are supreme real-time optimizing strategists. Implementing supposition of states digitally in a Digital Quantum Computer allows a program to avoid evaluating all routes to an answer. Software can be written to absorb the stock market and predict the outcome of all strategies programmed into it against all the data arriving from real-time data feeds. Once again, we need to be really careful about what we mean by this. In order for all answers to be evaluated, there needs to be 'machinery' that allows each outcome to become a possibility. So while the hardware exists to allow all desirable possibilities, when a choice is made, it is done in one step without evaluating all the other options for each quantum bit.
- Decision making in a Digital Quantum Computer runs many orders of magnitude faster than a conventional computer using the same amount of silicon with use of supposition of states.
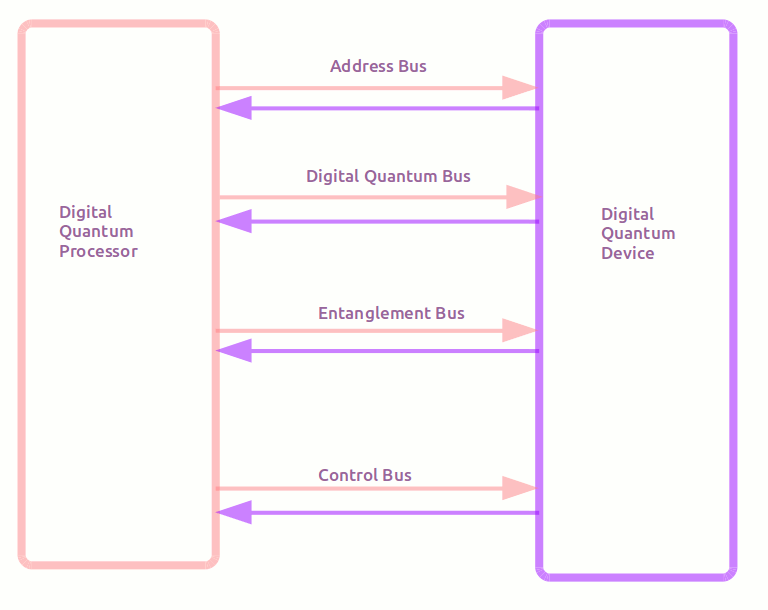
- First hint at what might be the world's first Digital Quantum Computer might look like is drawn in above figure.
- The buses are all asynchronous and bidirectional. Hence there is a need to duplicate the bus in each direction for best speed. To save on hardware any bus may be multiplexed to carry the bidirectional data, or the data from other buses with additional control lines.
- The address bus is similar to the address bus in a normal computer. The attached devices can talk back to a quantum computer without the need for traditional styles of arbitration for the code to work correctly.
- The Digital Quantum Bus is similar to a data bus. The similarity ends there. The data that moves in the Digital Quantum Bus is determined by resolution of the quantum states modeled. So if using 8 bit resolution, then the Digital Quantum Bus is 8 bits wide. A lot of data is variable in size. To indicate the resolution, a separate bus size information control lines are present in the control bus. So the Digital Quantum Bus may be 32 bits wide, but only uses 4 bits if the resolution bits in the control bus indicate it. The remaining bits do not toggle to save energy. Smaller resolution quantum bits move through a CPU a lot faster than quantum bits that have high resolution. Smaller resolution bits can be clocked faster to drain more energy to go faster in exchange.
- The Entanglement Bus is entirely new. It helps synchronize events without clocks being needed. Software has no idea of the Entanglement Bus or what it does. So developers have no need to worry about how their software is implemented. Software could be executing throughout a large collection of Digital Quantum CPUs, and where execution is to synchronize, it is completely automatic. Digital Entanglement is a huge step forward in computing. The actual hardware is about 5% to 10% more than a traditional CPU to implement entanglement. But the performance gain is thousands of percent over a conventional CPU design.
- The control bus is like any other in standard CPU design. There are control lines that control the bus and how devices talk to each other without tripping up.
- The interface between Digital Quantum CPU and peripherals is the same regardless of device. The number of bits and multiplexing may differ, but from a software perspective, and to a large extent the hardware perspective, all interconnect between devices follow the same 4 pair bus ideas. Even if all of that was squashed down to a one wire protocol, the actual perception from a code point of view is always the same physical model. Different vendors can modify the pin configurations, speed of IO lines, and may be even create a richer control bus, but ultimately, it must all work in the same way for the software to work correctly.
- The huge surprise is that only 3 basic commands need to be implemented for the Digital Quantum Computer to work. Three is not such a big number, and so our advise to all vendors is stick to an agreed model of binary compatibility and everyone's code will work on every machine without the traditional need to port code around from one CPU to the next.
- Because there are only 3 commands to implement, ideas of implementing functionality in microcode get washed away and is replaced with a collection of logic gates.
- What ALU functions are implemented is down to each individual manufacturer. It can be offloaded to a different chip. A different chip allows lesser CPUs to share the ALU as and when it is needed. It hardly makes any difference to speed of operation of typical data processing problem computations. The only time where it will make a difference is intensive like graphics rendering. But there again, most of the data is programmed and pipelined into systolic arrays - so more than one graphics processor will always improve performance without the need for Digital Quantum Computer to get involved.
- There is possibility of using microcode to control the ALU, but this may be down to either a lack of absorbing all the details on how best to implement ALU in a Digital Quantum way, or simply that it is currently the best solution for a lot of arithmetic functions to be packed around the ALU registers.
- With the availability of entanglement bus, it is also possible to compute with non-existence. This is similar to computing with 0's except in the quantum world it means the absence of existence. When non-existence is being processed, the Quantum Data Bus has no data but entangled bus does have entangled data. It can dramatically speed up database type of computations. Imagine for example searching for address of a person, it can now come back as something, null, or non-existent. Something that is valid is existent and would send data down the quantum data bus, something that is null is a field that has not been initialized but still sends data down the quantum data bus while non-existent means something totally different which in this case could be used to mean that the field is not part of the table. Computing with non-existence has potential for extreme data reduction because existence is not a value like null or 0 written into the data that takes up space.
- Another example of non-existence with a database query. The return can be the number of matches, 0 if there are none, null if the fields are not set, and non-existence if there are no matches to report. In this case 0 and non-existence is similar but not same. If the query function is designed to return 0, then that has to be sent through the Quantum Data Bus and processed as if it were any other number costing time and energy to be spent. If on the other hand the function returns non-existence signal, and then if the corresponding thread has code to understand non-existence, then on seeing non-existence signal, the Entanglement Bus communicates a non-existence signal, nothing passes through the Quantum Data Bus, and the corresponding function moves to the next operation in roughly one to two instruction 'cycles'. The calling function did not have to directly process a return parameter of the traditional kind. This is definitely a Digital Quantum Computer thing and not a Von-Neumann type of thing.
- (Because existence/non-existence is something useful in Digital Quantum Computer, it is likely that it has an equivalent in the Quantum Computer world. In physics non-existence could be used to mean physics rule violation. For example, jumping to a new energy state that is not permitted. So it hints that some type of processing could be gained from a Quantum Computer if part of the problem was programmed to exploit non-allowed states as a way of forcing the solution space to discard invalid answers more quickly.)
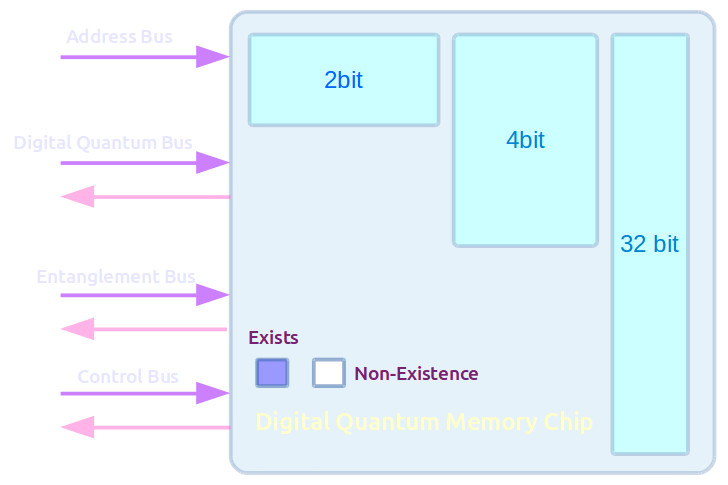
Digital Quantum Memory Chip Design
- The Quantum Data Bus has variable size data and hence the memory is also organized as variable sized bits. Large numbers of small word sizes frequently needed. As the word size increases, fewer storage elements required in those big sizes. Hence the memory can be optimized by arranging it to cater for a large number of more smaller word sizes. These smaller word sizes can operate faster than larger word sizes because there is so much less capacitive fanout loads that need to be driven. This can be traded to save power.
Digital Quantum Computer v AI
- Digital Quantum Computers 'think' through their states and state transition.
- Implementing Digital Quantum Computer as a simulation leads to surprising numbers. A 70MHz CPU can execute minimum 1 million instructions per second but make 100 million to 1 billion decisions per second. This is a little unexpected. By extension, A 1GHz ARM SoC could potentially make 1 trillion decisions per second. That is faster than ANY AI systems of today. Naturally there is no way to use all this power, so we find simulation of the Digital Quantum Computer spends most of its time idle!
- This result inspires us to make next generation mechatronics systems with Digital Quantum Computers or their simulations as they are likely to make it work better and faster than any current methods of programming. (This requires supporting CPUs with more internal flash memory to get more products built.)
- A real Digital Quantum Computer chip with about the same amount of electronics as an ARM SoC would be so powerful that it would take on any supercomputer and win at any AI game.
- A real Digital Quantum Computer chip with about the same amount of electronics as an Intel chip would be so powerful that it would take on an array of supercomputers and win over any scenario application.
- One Digital Quantum Computer chip about the size of an Intel CPU could probably simulate the entire population of London and all its vehicles many times over to predict crowd behavior in real time.
Simulating a real event in real time
- Imagine something happen in London and then we want to know how will the 8 million crowds and traffic behave. How should we change the traffic lights to divert traffic away from the area without least congestion? What should we be telling Police Officers to say to divert people and traffic from affected areas without jamming up the whole system or creating even more panic? A few dozen Digital Quantum Computer chips could simulate all the scenarios in real time, and select the best messages for traffic wardens to police and to road messaging boards for best optimal real time response.
Solving Complex Problems
- Factoring primes, solving optimization problems (quantum annealing), Fourier transforms etc can be solved by Digital Quantum Computer in one 'clock cycle' but all is not what it seems. In the quantum world nature throws up a wall against such fast computation by demanding ever greater cooling and averaging to remove noise to get precision. In the digital quantum world, temperature and noise considerations do not apply but as soon as precision is increased the hardware is doubled unlike a classical digital computer where hardware size grows very slowly while computing times increase exponentially instead. So the trade off for these 3 types of computers looks like this:
- Quantum Computing - low hardware requirement, exponential cooling requirement, near instant computation if averaging kept at constant duration and cooling provides the precision
- Digital Computer - low hardware requirement, no cooling, no averaging, exponential time required for greater precision
- Digital Quantum Computer - exponential hardware requirement, no cooling, no averaging, near instant computations
In short, in our universe that we live in, anyone building any kind of computer can trade cooling apparatus for hardware size against time to complete a computation.
Strange as that result sounds, it glimpses a fact - that there are no satisfying advantages to be gained from any type of computer that can be built to solve complex problems. If we try to get around this 'rule', nature throws up a wall and either demands infinite time, infinite cooling or infinite hardware to make gains. For practical gain, we would avoid 'infinite time' solution. Then the choice is between infinite cooling and infinite hardware. 'Infinite cooling' is just within reach of technology. 'Infinite hardware' is commonly available.
Elliptic key cryptography is another class of problems that cannot be defeated by quantum computers because there is no accuracy worth speaking of to solve recursive functions (solutions face problems similar to butterfly effect).
Likewise quantum computers cannot defeat 'block chain security'. The keys are public, so there is nothing to defeat. Each new member of the chain is dependent on the previous member, of which there are multiple copies and so there is nothing that can be done to forcefully change all copies other than break into each computer and alter them simultaneously - but that would be impossible with so many public peers to anonymous peers keeping copies of the data and working with it to create new records on the fly.
2018-11-16 - Digital Catapult Facilitated Quantum Computing Meet Up In St Hugh’s College, Oxford
- Listening to all the experts, UK heads world leading effort in Quantum Computers. Quantum computing has advanced to the stage where several Qbits are routinely manufactured to perform computations
- There are practical machines that solve optimization problems, cryptography, sensing etc
- But everyone agree there is a long way to go to solve Big Data problems because there is need for huge numbers of Qbits, and the need to find a way to load problems into a quantum computer
- There needs to be programming language that is easy to use that anyone can program problems into a quantum computer
- Comparing all that progress with Digital Quantum Computer, the ideas of Digital Quantum Computers ideas to simulations are light years ahead :)
- It would be possible to build a small ARM like processor with 5% extra Silicon that performs 1000 faster than conventional chip and could easily ship a billion units a year to displace weaker CPUs in traditional applications such as mobile phones, hand held devices, gaming devices, servers, PCs etc.
- A programming language with 3 commands (the remaining commands being flat function calls) exists for Digital Quantum Computer. There are no goto, if..then..else, do loops etc in this language because it is a Digital Quantum Computer. It is however Turning Complete (if you choose to write software thinking it through that way) and it is better than C programming language for writing real time applications normally written in C.
- Digital Quantum Computer easily allows Big Data to be loaded into the computer to solve every day problems.
- It could also solve in real time frequency and power allocation for 5G spectrum
- It could also satellite transponders and how they are switched on and off (managing power and co-channel interference) when passing over each territory.
Quantum Reality
- At some point quantum reality will need to be addressed when building a Digital Quantum Computer. This is down to how a Digital Quantum Computer is forced to interpret supposition of all states.
- The best way to describe quantum reality from attempting to construct a Digital Quantum Computer is to look at the double slit experiment.
- The packets of information we collect in a double slit experiment is down to the way information collection is molded by the experiment. This hints at a different interpretation of peaks and troughs.
- The reality of peaks and troughs measured do not mean that photons are present or absent at the measurement point. It is how the information is extracted at that point is what is changing.
- So varying the experiment in numerous ways could alter the collection of information at that point including moving the peaks to where troughs are and vice versa with all shades in between.
- This immovable interpretation is down to Digital Quantum Computer being able to take on all states but collapsing to one state when asked to do so. It does so in a way that is consistent with the inputs - not down to randomness. Exactly as Einstein claimed but revealed in a completely different interpretation of truth.
- In lay man speak, it is the shape of the detector (i.e. what it is made from, geometry of the sensor entrance, and directionality) that selectively determines what gets detected from all detection possibilities.
- Another deep challenge for quantum reality is interpretation of the need for entanglement in a quantum world.
- From a Digital Quantum Computer version of reality, entanglement is required so that every operation may run without error.
- Without digital version of entanglement, Digital Quantum Computers would error.
- Without entanglement Digital Quantum Computer could run at unimaginable unlimited speeds but with maximal error.
- In the real world, when universe was born, when did entanglement come into existence and why?
- The need for digital entanglement suggests entanglement was born into the quantum universe just at the point when inflation ended.
- This assumes just before inflation ended, an extremely large number of quantum computationally relevant things happened with computational error approaching maximal error.
- The purpose of entanglement was to limit the speed at which computations take place to the speed of light.
- The purpose of entanglement is to prevent the maximal quantum computational error condition and a run away universe.
Visions of the future
- When manufactured, a Quantum Processing UnitTM (QPU TM) is similar to CPUs and comes on a dice. However QPUs are smaller and faster than von-Neuman type of CPUs.
- The interfaces of QPUs require that peripherals use an entangled bus which is less prone to error, serial in design, and running at fastest possible speeds.
- Parallel implementation of buses likely not supported. Multiple serial links can multiply communication speeds instead.
- Peripherals can implement their own QPUs to connect to QPU entangled bus and process data which is safer with less hardware overhead than raw access into a QPU which has incredibly high data processing rates of entangled data.
- A PC of the future will become a PDTM (Personal Data Center TM) with 100gbit link or faster.
- A good use of a PD is to process the huge amounts of data from Smart Cities, Smart Factories and Supply Chain.
- A data center of PDs would work more efficiently than current data centers with slow PC connectivity.
Exciting times ahead... This subject still has missing pieces and remains a giant puzzle to solve... More to follow...
|